This method of solving sudoku describes a search of an only candidate for a cell. Most people begin solving sudoku of easy and average difficulty levels with this method. It has several modifications, and I’m going to tell about each of them one by one. And since describing sudoku solving in words is difficult, I have prepared explanatory illustrations for you.

Singleton in a square

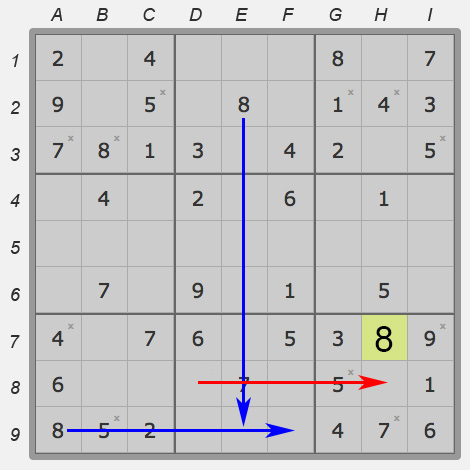
A puzzle of average difficulty is suitable for this method.

On the picture below we will try to find place for eight. Using the main sudoku rule, we find the conditions we need:

• Cell G:9 crosses out line 1.
• Cell E:2 crosses out line 2.
• Cell A:9 removes column A.

These three conditions are enough to indicate that the only place left for eight is cell B:3. It means we have found a singleton for a cell. We can put eight there without any doubt.

Hopeless singleton in a column or line

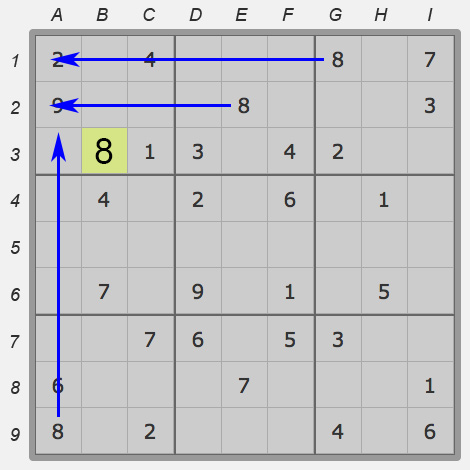
We continue to fill in our sudoku. The point of this method is to identify an only candidate for a cell. The main difference from the previous method will be not an exclusion (of lines, columns) but a prohibition for a certain column.

In this example, let’s look at column A. Only five of its cells are empty. Here are several useful conditions

• Cell C:1, which contains four, forbids to insert in A:3.
• Cell B:4 also forbids to put four in cells A:4, A:5, A:6.

The only “free” cell left is A:7. So we’re putting four in it.

“Insecure” singleton

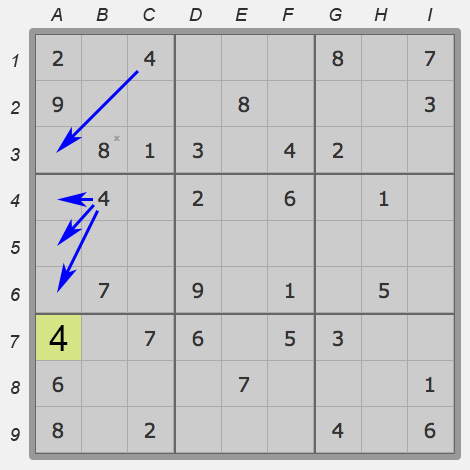
I call this method insecure since we already see several conditions for the search of a singleton, but we lack one condition to insert a number in a cell for sure. However, this condition exists – we only need to find it. While we are looking for it, the singleton remains insecure. Now more details about the method.

In the last square we have two empty cells. We are ready to fill in two last numbers, but it isn’t so easy. Each of these cells has got two candidates – 2 and 8.

Let’s try to lead our situation to the hopeless singleton.

• Cell E:2 crosses out column E.
• Cell A:9 crosses out line 9.

As a result, in the eighth square (middle lower) eight has to be in cell D:8 or F:8. It means that this square completely crosses out 8th line.

This is enough for us. We can confidently insert “insecure” eight in H:7.